POST-DOCTORATE PROPOSAL

Reference : PDOC-Département-Année de sélection-Numéro d'ordre (to be recalled in all correspondence) 

Start of contract: November/December 2024

 Application deadline: Duration: 12 months, possibly extendable to 18 months - 

Gross yearly salary: about 38 k€ (medical insurance included) 

Keywords: Reduced basis method, order reduction, model reduction, finite element method, electromagnetism, aeroacoustics Profile and skills required PhD thesis in applied mathematics, knowledge in acoustics and/or electromagnetism and more generally in wave physics is appreciated Presentation of the post-doctoral project, context and objective The evaluation of acoustic installation effects (masking, reflection, etc.) is essential to assess the acoustic impact of aircraft at the ground level, in particular in the context of acoustic certification. In addition, evaluation and certification have to address the entire audible frequency bandwidth. These issues arise during the design stage of new aircraft architectures, during which several acoustic source locations (e.g. the engine) are studied to achieve acoustic optimization. In electromagnetism, radar imaging is essential to precisely analyse the interactions between a wave and a target. To obtain a useful radar image (in terms of localization and resolution), it is necessary to measure or calculate a significant number of frequencies and incidence angles depending on the target’s length and the observation and analysis domain. Successive electromagnetic propagation problems associated with plane waves must be solved for each frequency and incidence angle. 

The Boundary Element Method (BEM) is commonly used for acoustic studies, especially for evaluating the masking effects of new aircraft architectures, and for electromagnetism studies to simulate the radar signature of an object. Even with efficient numerical methods employed to accelerate BEM computations, the overall computational cost of frequency sweeping is unaffordable due to the significant number of frequencies that need to be solved independently of each other. In this context, the reduced basis method has attracted much interest in the past ten years and is a very active research topic nowadays. It allows to approach the solution depending on one or several parameter(s) by using solutions obtained on a limited number of parameters values, has shown increased appeal for around ten years and is now a very active research subject. In practice, the reduced basis construction algorithm calls a BEM solver (acoustic or electromagnetic) as an external service. If the parameter of interest is the frequency, then the reduced basis method minimizes the number of frequencies for which a BEM resolution (i.e. matrix building and iterative resolution of the linear system) is needed to sweep the frequencies, thus decreasing the overall computational cost (likewise if the parameter under consideration is the incidence angle). Compared to a classical resolution (one computation per frequency and/or incidence angle), the cost-saving is all the more significant that both parameters are considered simultaneously. 

The results from P. Edel’s PhD thesis at ONERA allowed for the development and the implementation of the reduced basis method for handling multiple frequencies and multiple incidences in electromagnetic diffraction problems. The problems were solved using surface integral equations discretized by the boundary element method. The implementation considered only perfectly conductive materials, though. Figure 1 displays the radar imaging results obtained from the reduced basis method algorithm, which was implemented during P. Edel’s PhD thesis. These results were achieved with 101 frequencies and 121 incidence angles, and they demonstrated a computational speed approximately 1.5 times faster than the conventional approach. 

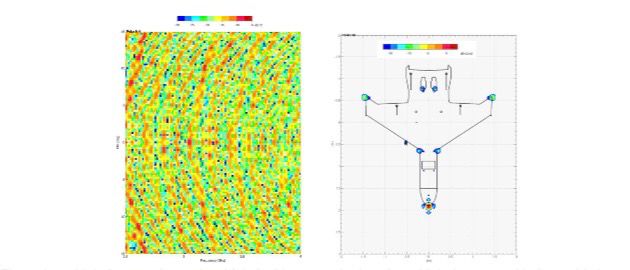
Figure 1: multiple frequencies and multiple incidences radar imaging with hologram and holographic image 

The post-doctorate associate will have a dual objective: 

1. Extend the reduced basis method for electromagnetism: 

a. To non-perfectly conductive objects with surface impedance, thick materials (integral equations/volume finite elements coupling) 

b. To excitations other than plane waves (e. g. tension generator modelled by a monopole) 

2. Extend this method to aeroacoustics, in particular: 

a. To operator specific to acoustics (nodal values vs. current between two edges) 

b. To the uniform flow case 

c. Evaluate the influence of the matrix-vector products and of the matrix building, with the MultiLevel Fast Multipole Method (MLFMM) or the Hierarchical Matrix method (H-Matrix) which are the two services (with computational and memory costs) called by the reduced basis algorithm 

d. Evaluate the influence on the performances and the precision of the results of the error estimator considered by the method to evaluate and control the induced error e. Consider other parameters than the frequency, e. g. the source location, the location and/or value of the impedance boundary condition… 

Bibliography: 

• P. Edel, Reduced basis method for parameter-dependent linear equations. Application to time-harmonic problems in electromagnetism and in aeroacoustics, PhD thesis 2022. 

• M. Fares, J. S. Hesthaven, Y. Maday, and B. Stamm. The reduced basis method for the electric field integral equation. Journal of Computational Physics, 230(14):5532–5555, 2011. • M. Barrault, Y. Maday, N. C. Nguyen, and A. T. Patera. An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathématique, 339(9):667–672, 2004. 

External collaborations Host laboratory at ONERA 

Department : Aérodynamique, Aéroélasticité, Acoustique 

Location (ONERA centre): Châtillon 

Contact: Mathieu Lorteau, Jérôme Simon 

Phone: +33146734388 

Email : mathieu.lorteau@onera.fr, jerome.simon@onera.fr